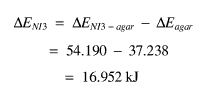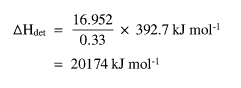1.7 Steel bomb calorimetry
Calibration
Calibration of the bomb calorimeter is performed by detonating a known quantity of AR grade benzoic acid under 25 atmospheres pressure oxygen with the bomb being kept inside of a thermostated jacket of circulating water. The circulated water jacket is to keep the temperature of the water surrounding the bomb at a constant temperature.
The mass of benzoic acid needs to be known to 4 decimal places. Also, the mass of the cotton used as the fuse must be known as this too will have a calorific value.
The literature value for delta Hc benzoic acid is 26.435 kJ g-1 (3228.3268 kJ mol-1) with an energy equivalent, W, for the calorimeter of 10.7609 kJ K-1.
The temperature readings in the tables below are from a Beckman thermometer. This type of thermometer normally ranges from between 0 to 6°C, is highly accurate and can be adjusted to make reading a temperature simpler. The temperatures are all therefore relative to the initial temperature taken by the Beckman thermometer.
| Time (secs)
| Temp (°C)
|
| Time (secs)
| Temp (°C)
|
| 0.00
| 1.005
|
| 23.00
| 3.560
|
| 3.00
| 1.020
|
| 23.15
| 3.620
|
| 6.00
| 1.040
|
| 23.30
| 3.660
|
| 9.00
| 1.060
|
| 23.40
| 3.700
|
| 12.00
| 1.080
|
| 23.50
| 3.730
|
| 15.00
| 1.100
|
| 24.00
| 3.770
|
| 18.00
| 1.130
|
| 24.15
| 3.785
|
| 21.00
| 1.150
|
| 24.30
| 3.800
|
| 21.10
| 1.160
|
| 24.40
| 3.810
|
| 21.20
| 1.250
|
| 24.50
| 3.820
|
| 21.30
| 1.580
|
| 25.00
| 3.830
|
| 21.40
| 2.080
|
| 26.00
| 3.850
|
| 21.50
| 2.380
|
| 27.00
| 3.855
|
| 22.00
| 2.630
|
| 28.00
| 3.855
|
| 22.10
| 2.990
|
| 29.00
| 3.855
|
| 22.20
| 3.160
|
| 30.00
| 3.850
|
| 22.30
| 3.280
|
| 31.00
| 3.845
|
| 22.40
| 3.400
|
| 32.00
| 3.840
|
| 22.50
| 3.490
|
| 33.00
| 3.835
|
|
|
|
| 34.00
| 3.835
|
|
|
|
| 35.00
| 3.830
|
Table 1. Calibration data for benzoic acid, mass 1.0870g
When plotted, this gives the following graph

Calculations
T1 = 1.005 t1 = 0
T2 = 1.15 t2 = 21
T3 = 3.855 t3 = 26.5
T4 = 3.81 t4 = 44



qi and qn are the thermal contribution of the cotton and fuse wire respectively.
As these values are for approximately 1g of benzoic acid, it is far simpler to compare the results from the experiment to the calibration results, gram to gram. This saves a great deal more time than for the constant re-calculation of each sample.
The graphs
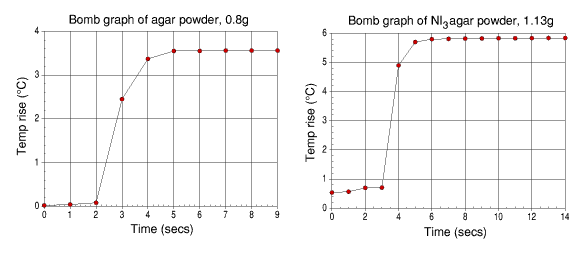
It can be seen from both of these graphs that the amount of energy released per gram by both the dry agar and the dry NI3 agar powder are rather high and considerably more than for the benzoic acid, though this is not true for the agar powder itself.
Calculation of energy release
It has already been show how to calculate the both the energy equivalent and from (1) the total energy is derived.
|
|
| Agar powder
|
|
|
|
| Agar / NI3
|
|
| t1
| 0 s
| T1
| 0.02
|
| t1
| 0 s
| T1
| 0.54
|
| t2
| 2 s
| T2
| 0.08
|
| t2
| 3 s
| T2
| 0.71
|
| t3
| 5 s
| T3
| 3.55
|
| t3
| 12 s
| T3
| 5.385
|
| t4
| 9s
| T4
| 3.56
|
| t4
| 14 s
| T4
| 5.84
|
|
|
| Tr
| 0.49
|
|
|
| Tr
| 2.64
|
(T = °C, t = seconds. Tr calculated by the Simpson rule (see equation (14))
Calculating these out with the formulae above yield the following results
| Sample
| Agar
| NI3
|
|
|
|
| T1
| 0.020
| 0.540
|
| Mass (agar)
| 0.800 g
|
| T2
| 0.080
| 0.710
|
| delta T (agar)
| 3.460
|
| T3
| 3.550
| 5.835
|
|
|
|
| T4
| 3.560
| 5.840
|
| delta E / kJ
| 37.238
|
| t1
| 0.000
| 0.000
|
|
|
|
| t2
| 2.000
| 3.000
|
|
|
|
| t3
| 5.000
| 12.000
|
| Mass (NI3)
| 1.130 g
|
| t4
| 9.000
| 14.000
|
| delta T (NI3)
| 5.036
|
| Ra
| 0.003
| 0.002
|
|
|
|
| Rf
| 0.030
| 0.057
|
| delta E / kJ
| 54.190
|
| Ta
| 3.555
| 5.838
|
|
|
|
| Tf
| 0.050
| 0.625
|
|
|
|
| Tr
| 3.47
| 5.125
|
It is obvious from the results that both NI3 - agar and agar alone give off far more energy per gram than AR benzoic acid.
However, it should also be remembered that the NI3 is in agar. The actual mass of agar was the same as for the agar / NI3 sample itself, therefore if the difference is taken between the two delta E values (as well as between the masses), the final figure for NI3 will be
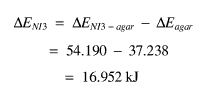
This energy term can be related to delta H as all energy changes within the bomb are delta E values . By using

where n is the number of moles of gas evolved and T is the average run temperature . The †nRT term will be negligible here.
If the delta E value is divided by 0.33 (the mass of NI3) then multiplied by the R.M.M. of dry NI3 (392.7), delta Hdet is found.
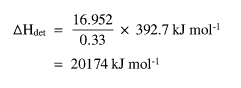
This value is far higher than the value of delta Hf NI39 (287 ± 23 kJ mol-1).
9 Davies, R.H., Finch, A., Gates, P.N. The Standard Enthalpy of Formation of Nitrogen Tri-Iodide Monoammine and the Nitrogen Iodine Bond Energy.J. Chem. Soc - Chem. Comms, 1989, No. 19, pp 1461 - 1462.
For an energy release of such an order above that of the published value for †
delta Hf, the nature of the type of bond in NI3 comes into question. While there is no doubt that there is a bond of some description, the sheer size of the iodine atoms in comparison to that of the central nitrogen atom would suggest large bond lengths and a high degree of sp or pd hybridisation. The bond would also have a substantial degree of anti-bonding character. The bond energy would be expected to be low.
In dealing with a molecule of this type, consideration of bond energies is not enough. As each nitrogen - iodine bond is broken, the remained iodine atoms are drawn closed to the nitrogen ion. This results in a far shorter bond length which requires more energy to break the remaining bonds. The energy required to break the second and third N - I bonds would have to be higher with the final bond energy a more typical figure.
Glass calorimetry. Method 1.8
1. Speed of heat transfer from the glass calorimeter to water.
The rate at which the glass transmitted heat to the water was required to ensure a rapid enough response. The thermal capacity of the polystyrene cup was considered to be negligible. If the heat transfer rate is not fast enough, the experimental data recorded will be not accurate enough.
The computer program was started. The bomb was filled with water at 25°C, placed into the cup and water at 20°C poured around it. The lid was quickly placed on and the time taken for the temperature to rise by 1°C recorded. This was repeated three times.
| Run number
| Time taken for 1°C rise
|
| 1
| 6 seconds
|
| 2
| 5.8 seconds
|
| 3
| 6.3 seconds
|
|
|
|
|
|
|
The transmission of heat to the water was considered to be rapid enough for the calorimetry. A slow time would indicate that the heat transfer across the glass would not be rapid enough and substantial cooling may occur within the bomb. The water would also warm far slower giving a false depiction of the calorimetric experiment in progress. A rapid heat transfer would indicate the reverse.
2. Calibration and work equivalent
Using the same method as in 1.7 (except for the extreme O2 pressure), the glass calorimeter was calibrated using 0.2g benzoic acid.
The following results were obtained.
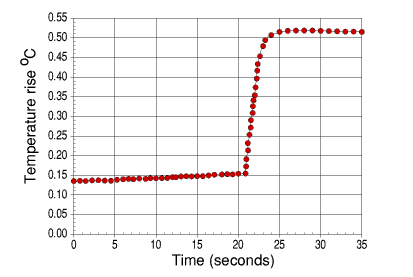
Graph of calibration curve for benzoic acid using the glass calorimeter.
| Time (secs)
| Temp (°C)
|
| Time (secs)
| Temp (°C)
|
| 0.00
| 0.135
|
| 23.00
| 0.479
|
| 3.00
| 0.137
|
| 23.10
| 0.487
|
| 6.00
| 0.140
|
| 23.25
| 0.492
|
| 9.00
| 0.143
|
| 23.38
| 0.498
|
| 12.00
| 0.145
|
| 23.50
| 0.502
|
| 15.00
| 0.148
|
| 24.00
| 0.507
|
| 18.00
| 0.152
|
| 24.10
| 0.509
|
| 21.00
| 0.155
|
| 24.30
| 0.511
|
| 21.10
| 0.156
|
| 24.40
| 0.512
|
| 21.20
| 0.168
|
| 24.50
| 0.514
|
| 21.30
| 0.213
|
| 25.00
| 0.515
|
| 21.40
| 0.280
|
| 26.00
| 0.518
|
| 21.50
| 0.320
|
| 27.00
| 0.518
|
| 22.00
| 0.354
|
| 28.00
| 0.518
|
| 22.10
| 0.402
|
| 29.00
| 0.518
|
| 22.20
| 0.425
|
| 30.00
| 0.518
|
| 22.30
| 0.441
|
| 31.00
| 0.517
|
| 22.40
| 0.457
|
| 32.00
| 0.516
|
| 22.50
| 0.469
|
| 33.00
| 0.516
|
|
|
|
| 34.00
| 0.516
|
|
|
|
| 35.00
| 0.515
|
The temperature rise was calculated via the computer program by taking the new temperature reading of the water from the initial temperature reading of the water.
From the calibration data
| T1
| 0.073
|
|
|
|
| T2
| 0.095
|
|
|
|
| T3
| 0.785
|
|
|
|
| T4
| 0.785
|
| Mass (g)
| 0.20
|
| t1
| 0.000
|
| delta T
| 0.688
|
| t2
| 0.403
|
|
|
|
| t3
| 1.614
|
|
|
|
| t4
| 1.883
|
|
|
|
| Ra
| 0.000
|
|
|
|
| Rf
| 0.008
|
|
|
|
| Ta
| 0.785
|
|
|
|
| Tf
| 0.084
|
|
|
|
| Tr
| 0.689
|
|
|
|
The work equivalent, W, was calculated on the basis of this data and gave a result of 7.7955 kJ K-1.
3. Calorimetry
The computer was reset and the program restarted. A known mass of NI3 was placed into the glass calorimeter, the calorimeter sealed and placed into the polystyrene cup, which was sealed also. The spark was introduced and temperature rise observed. The following results were observed for three different samples.
The delta Hdet (NI3) was calculated using the same method as for the steel calorimeter results.
| Sample
| 1
| 2
| 3
|
| T1
| 0.25
| 0.31
| 0.18
|
| T2
| 0.43
| 0.50
| 0.35
|
| T3
| 2.53
| 2.57
| 2.11
|
| T4
| 2.54
| 2.58
| 2.12
|
| t1
| 1.000
| 1.000
| 1.000
|
| t2
| 2.700
| 2.600
| 2.650
|
| t3
| 6.000
| 6.150
| 5.800
|
| t4
| 6.100
| 6.500
| 6.000
|
| Ra
| 0.100
| 0.029
| 0.050
|
| Rf
| 0.106
| 0.119
| 0.103
|
| Ta
| 2.535
| 2.575
| 2.115
|
| Tf
| 0.340
| 0.405
| 0.265
|
| Tr
| 2.100
| 2.070
| 1.760
|
| Mass (g)
| 0.30
| 0.32
| 0.27
|
| delta T
| 1.77
| 1.89
| 1.57
|
| delta E / kJ
| 13.77
| 14.77
| 12.24
|
| delta Hdet kJ mol-1
| 18022.51
| 18120.63
| 17806.82
|
|
|
|
|
|
delta Hdet is for the dry NI3 (R.M.M. 393). The accuracy of this method gave a higher degree of reproducibility.