
5. The use of sound as a detonator
5.1 Theory
Nitrogen triiodide is sensitive to shock. A shock can be considered as the movement of air at a particular frequency. Normally, a shock wave in air is detected using a microphone connected to an oscilloscope. This will produce a wave on the screen and by selecting the correct attenuation on the scope, will give a wavelength.
However, a shock wave cannot be considered as a single sound wave. It is more common that any shock will be the culmination of a number of sound waves interacting with each other (much as in the same way as a voice is not a single sound). As a method of determining the correct amount of energy for the detonation, it will not be of any use.
By using a signal generator connected to a suitable loudspeaker, it is possible to determine the correct frequency needed to trigger detonation of a sample.
The sample will have two natural types of vibration, harmonic and resonant (also known as the natural). The harmonic is that which will be in sympathy to the real (the two will combine to make a harmonic note. The real is the pure note.). When the signal generator comes to the correct frequency to cause the sample to detonate instantly, this will correspond to the resonance point. The harmonic will require time for the energy build up to occur.
5.2 Relation of sound to energy
All soundwaves normally will contain a range of frequencies. When there is a pure frequency, the amount of energy produced can be simply calculated using a relationship between the area of the sound sphere (the effective area the sound projects to), the power from the speaker, the distance the wave travels and the ratio of the area of sample to that of the sound cone.
The formulae which can be used for this are

Practically, however, the distance between each of the different wavelengths is small, so that for all intents and purposes, the distance between the sample and speaker for differing frequencies can be kept the same.
Using the system (as shown in diagram 9), the microphone was moved towards and away from the speaker until the sine wave on the oscilloscope reached its highest peak. This is the point of convergence of the sound waves. At this point, the energy supplied is at a maximum.
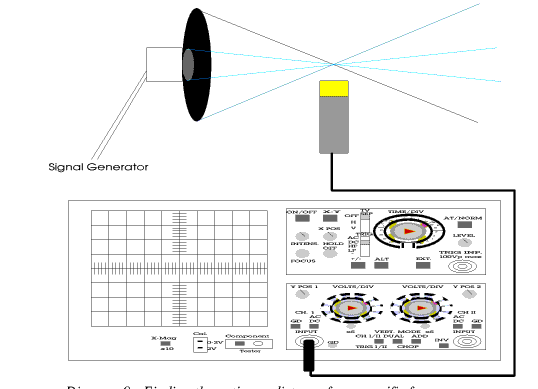
Diagram 9 - Finding the optimum distance for a specific frequency.
This distance between the speaker and sample is important as there is a direct relationship between energy, wave amplitude and distance. As the distance increases, the amount of energy provided by the signal decreases, so to keep the same amount of energy reaching the sample, the wave amplitude has to be increased. The converse applies equally.
The power of the speaker is measured by connecting a multimeter across the speaker with a signal being passed from the signal generator to the speaker at the same time. The speaker used had an internal amplifier circuit, so the measurements of voltage and current were taken on the circuit board but after the amplification of the signal.
Power is calculated using equation (22)
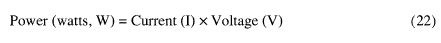
One of the main problems with any sort of sound measurement is the "standing wave". This is when the wave going "out" of the speaker interferes with the wave coming "back". This is shown to better effect in diagram 10. The standing wave is at the position marked "Node".
At this position, the air pressure is at a maximum. By using (23), the distance required for the standing wave at a given frequency can be calculated.
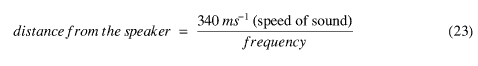
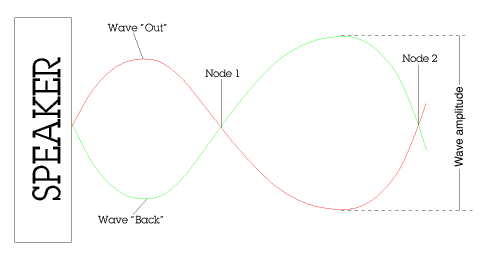
Diagram 10 - A demonstration of a standing wave
This distance is required for the area of the sound sphere. The distance will be divided by 2 to become the radius of the sound sphere. This distance is required for equation (20).
The sound wave is known as being incident to that of the sample. This means that the sound is directed onto the sample. Any sound which is not absorbed will be reflected from the sample. The degree of reflection will determine how much power has been absorbed by the sample.
The amount of reflection can be easily determined by placing a microphone at the same distance from the sample as the speaker, but at an angle of 45°. The angle is necessary to avoid interference from the sound coming from the speaker. The sound intensity reflected from the sample will be at a maximum between 30 and 60 degrees (assuming the speaker is at 90 degrees to the sample). The microphone is then connected directly to a high accuracy digital multimeter and the power reflected back calculated using (22).
